Research Topics (中文版本请点击这里)

Numerical Methods for Eigenvalue Problems

In this topic, we propose the multilevel correction method and augmented subspace method for solving eigenvalue problems. These two methods can improve the efficiency for solving eigenvalue problems to be almost the same as solving the corresponding linear boundary value problems. Especially, based on the multilevel correction method and augmented subspace methods, we can design a type of eigenwise parallel method for solving eigenvalue problems and there is no inner product computation during the eigenvlaue solving.

The augmented subspace method can be described as follows:

$\mathcal T_H$ $V_H$ ;
$V_H$ $(\lambda_H,u_H)\in\mathbb R\times V_H$ such that
$\begin{matrix} (1) & a (u_{H}, v_{H}) = λ_{H} b (u_{H}, v_{H}), \forall v_{H} \in V_{H} . \end{matrix}$
$\mathcal T_H$ $\mathcal T_h$ $V_h$ $u_h^{(1)}:=u_H$ $\lambda_h^{(1)}=\lambda_H$ $\ell=1$ and then do the following iterations:
$\widehat u_h^{(\ell+1)}\in V_h$ such that

\begin{matrix} (2) & a ({\hat{u}}_{h}^{(ℓ + 1)}, v_{h}) = λ_{h}^{(ℓ)} b (u_{h}^{(ℓ)}, v_{h}), \forall v_{h} \in V_{h} . \end{matrix}

We can use the efficient multigrid or domain decomposition method to the above linear equations.

$V_{H,h}=V_H+{\rm span}\{\widehat u_h^{(\ell+1)}\}$ $(\lambda_h^{(\ell+1)},u_h^{(\ell+1)})\in \mathbb R\times V_{H,h}$ such that
$\begin{matrix} (3) & a (u_{h}^{(ℓ + 1)}, v_{H, h}) = λ_{h}^{(ℓ + 1)} b (u_{h}^{(ℓ + 1)}, v_{H, h}), \forall v_{H, h} \in V_{H, h} . \end{matrix}$
$\ell:=\ell+1$ and go to Step 4 for the next iteration unticl convergence.

Roughly speaking, the above algorithm has following convergence rate

\begin{array}{rcl} (4) & ∥ {\bar{u}}_{h} - u_{h}^{(ℓ + 1)} ∥_{a} & \leq & C η_{a}^{2} (V_{H}) ∥ {\bar{u}}_{h} - u_{h}^{(ℓ)} ∥_{a}, \\ (5) & ∥ {\bar{u}}_{h} - u_{h}^{(ℓ + 1)} ∥_{b} & \leq & C η_{a} (V_{H}) ∥ {\bar{u}}_{h} - u_{h} ∥_{a}, \end{array}

$\bar u_h$ $V_h$ $\eta_a(V_H)$ are defined as follows

\begin{array}{r} (6) & η_{a} (V_{H}) = sup_{0 \neq f \in L^{2} (Ω)} inf_{v_{H} \in V_{H}} \frac{∥ T f - v_{h} ∥_{a}}{∥ f ∥_{b}}, \end{array}

$T: L^2(\Omega)\rightarrow H_0^1(\Omega)$ being defined as follows

\begin{matrix} (7) & a (T f, v) = b (f, v), \forall v \in H_{0}^{1} (Ω) . \end{matrix}

From (4), we can find that the augmented subspace method has second convergence order which is better than the first order corretion methods.

Based on the augmented subspace and the multilevel spaces from the multigrid method for the linear boundary value problem, we can define the multilevel correction method.

For more information, please refer to the following papers and softwares.

There are also the video class in 2022: 特征值问题数值算法讲义: 课程特征值问题数值算法的讲义, 相应的视频如下: 特征值问题数值算法视频1 (Bilibili网站), 特征值问题数值算法视频2 (Bilibili网站);

Papers:

Xiaole Han, Hehu Xie and Fei Xu, A cascadic multigrid method for eigenvalue problem, Journal of Computational Mathematics, 35(1) (2017), 7-90.
Shanghui Jia, Hehu Xie, Manting Xie and Fei Xu, A full multigrid method for nonlinear eigenvalue problems, Sci China Math, 59 (2016), 2037–2048.
Hehu Xie and Manting Xie, A multigrid method for ground state solution of Bose-Einetein condensates, Commun. Comput. Phys., 19(3) (2016), 648-662.
Hongtao Chen, Hehu Xie and Fei Xu, A full multigrid method for eigenvalue problems, Journal of Computational Physics,322 (2016),747-759.
Xiaole Han, Yu Li, Hehu Xie and Chunguang You, Local and parallel finite element algorithm based on multilevel discretization for eigenvalue problems, International Journal of Numerical Analysis & Modeling, 13(1) (2016),73-89.
Hehu Xie and Tao Zhou, A multilevel finite element method for Fredholm integral eigenvalue problems,Journal of Computational Physics,303 (2015),173-184
Hongtao Chen,Yunhui He, Yu Li and Hehu Xie, A multigrid method for eigenvalue problems based on shifted-inverse power technique. European Journal of Mathematics, 1(1) (2015), 207-228.
Xiaole Han, Yu Li and Hehu Xie, A multilevel correction method for Steklov eigenvalue problem by nonconforming finite element methods, Numerical Mathematics: Theory, Methods and Applications, 8(03) (2015), 383-405.
谢和虎, 非线性特征值问题的多重网格算法,中国科学：数学, 45 (8) (2015), 1193-1204. (Hehu Xie, A multigrid method for nonlinear eigenvalue problems (in Chinese), Sci Sin Math, 45 (2015), 1193-1204).
Qun Lin, Hehu Xie and Fei Xu, Multilevel correction adaptive finite element method for semilinear elliptic equation, Application of Mathematics, 60(5) (2015), 527-550.
Wei Gong, Hehu Xie, Ningning Yan, A multilevel correction method for optimal controls of elliptic equation, SIAM J. Sci. Comput., 37(5) （2015）, A2198-A2221, 2015.
Qun Lin, Fusheng Luo and Hehu Xie, A multilevel correction method for Stokes eigenvalue problems and its application, Mathematical Methods in the Applied Sciences, 38(18) (2015), 4540-4552.
Qun Lin and Hehu Xie, A multi-level correction scheme for eigenvalue problems, Mathematics of Computation, 84(291) (2015), 71-88.
Hehu Xie, A type of multilevel method for the Steklov eigenvalue problem, IMA J. Numer. Anal., 34(2) (2014), 592-608.
Hehu Xie, A multigrid method for eigenvalue problem, Journal of Computational Physics, 274(1), 2014, pages 550-561.
Xia Ji, Jiguang Sun and Hehu Xie, A multigrid method for Helmholtz transmission eigenvalue problems, Journal of Scientific Computing, 60(2), pages: 276-294, 2014.
Qun Lin and Hehu Xie (谢和虎), A multilevel correction type of adaptive finite element method for Steklov eigenvalue problems, Proceedings of the International Conference Applications of Mathematics 2012, pp. 134-143.
Qun Lin and Hehu Xie, An observation on Aubin-Nitsche Lemma and its applications, Mathematics in Practice and Theory, 41(17) (2011), 247-258.(In Chinese, English title and abstract)

Machine learning methods

In this topic, we propose a type of tensor neural network (TNN) for solving high dimensional problems. The TNN is a function being designed by the tensor product operations on the neural networks or by correlated low-rank CANDECOMP/PARAFAC (CP) tensor decomposition approximations of FNNs. An important advantage is that we do not need to use Monte-Carlo method to do the integration for the functions which is constructed by TNN. The high dimensional integration of the TNN functions can be decomposed into one-dimensional integrations which can be computed by the highly accurate Gauss type quadrature scheme. The computational work for the integration of the functions by TNN is only a polynomial scale of the dimension, which means the TNN overcomes the curse of dimensionality in some sense for solving high-dimensional PDEs. Furthermore, the high accuracy of high dimensional integration can improve the TNN-based machine learning methods for solving high-dimensional problems.

The number of layers and neurons in each layer, the selections of activation functions and other hyperparameters can be different in different subnetworks. TNN is defined as follows:

\begin{array}{r} (8) & Ψ (x; Θ) = \sum_{j = 1}^{p} c_{j} {\hat{ϕ}}_{1, j} (x_{1}; θ_{1}) {\hat{ϕ}}_{2, j} (x_{2}; θ_{2}) \dots {\hat{ϕ}}_{d, j} (x_{d}; θ_{d}) = \sum_{j = 1}^{p} c_{j} \prod_{i = 1}^{d} {\hat{ϕ}}_{i, j} (x_{i}; θ_{i}), \end{array}

$c=\{c_j\}_{j=1}^{p}$ $\Theta=\{c,\theta_1,\cdots,\theta_d\}$ $i=1,\cdots,d,j=1,\cdots,p$ $\widehat\phi_{i,j}(x_i,\theta_i)$ is a normalized functions as follows:

\begin{array}{r} (9) & {\hat{ϕ}}_{i, j} (x_{i}, θ_{i}) = \frac{ϕ_{i, j} (x_{i}, θ_{i})}{∥ ϕ_{i, j} (x_{i}, θ_{i}) ∥_{L^{2} (Ω_{i})}} . \end{array}

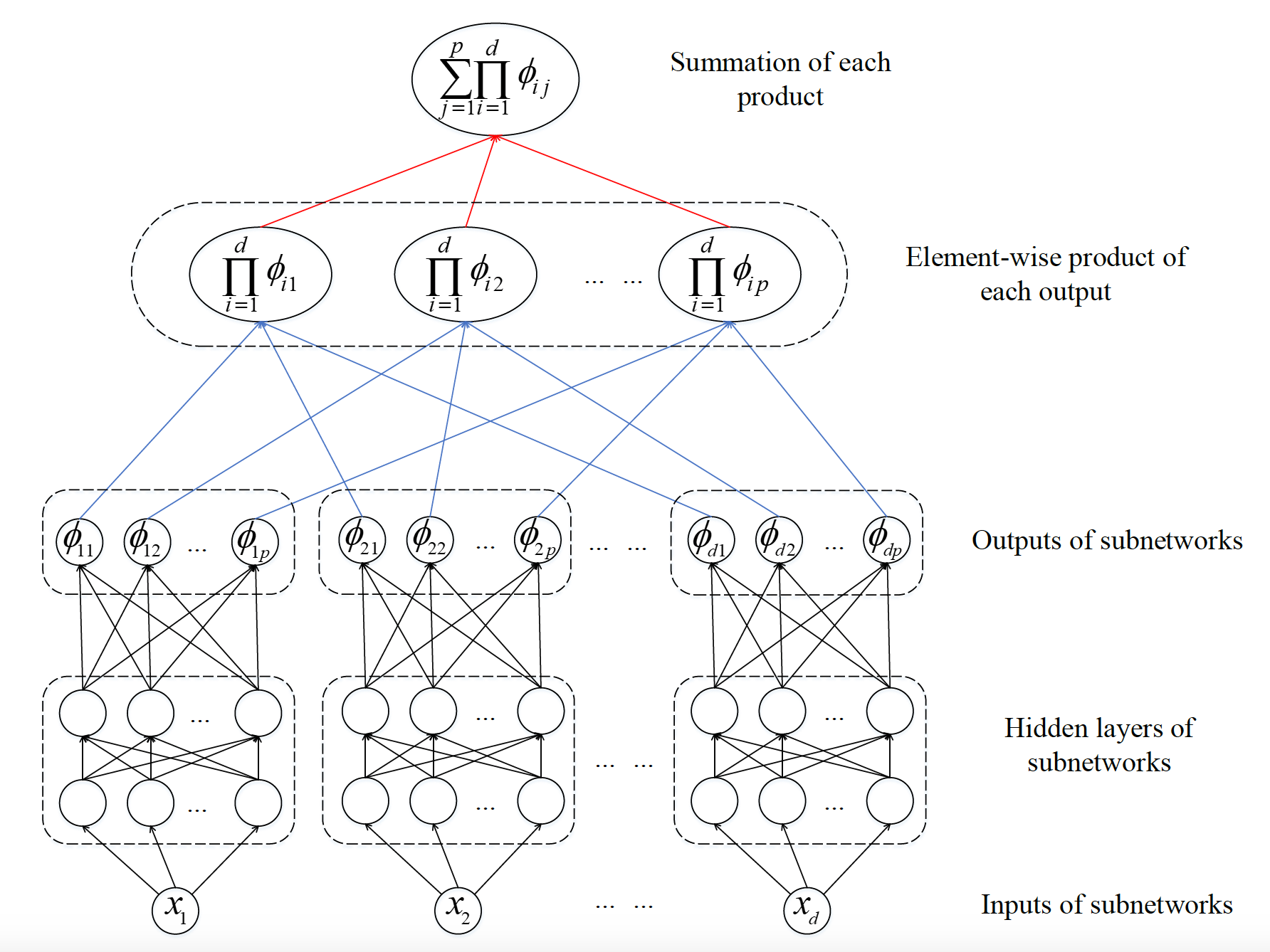
We can find the parameters for each rank of TNN are correlated by the FNN, which guarantee the stability of the TNN-based machine learning methods.

The TNN is also used to solve 20,000 dimensional Schr"{o}dinger equation with coupled quantum harmonic oscillator potential function in

Z. Hu, K. Shukla, G. E. Karniadakis and K. Kawaguchi, Tackling the curse of dimensionality 768 with physics-informed neural networks, arXiv:2307.12306v5, 2024,

high dimensional Fokker-Planck equations in

T. Wang, Z. Hu, K. Kawaguchi, Z. Zhang and G. E. Karniadakis, Tensor neural networks for high-dimensional Fokker-Planck equations, arXiv:2404.05615v1, 2024， and high dimensional time-dependent problems in

T. Kao, J. Zhao and L. Zhang, pETNNs: partial evolutionary tensor neural networks for solving time-dependent partial differential equations, arXiv:2403.06084v1, 2024.

$u$ such that

\begin{array}{r} {\begin{aligned} - Δ u & = (d + 3) π^{2} \sum_{k = 1}^{d} \sin (2 π x_{k}) \cdot \prod_{i \neq k}^{d} \sin (π x_{i}), & x \in & (- 1, 1)^{d}, \\ u & = 0, & x \in & \partial [- 1, 1]^{d} . \end{aligned} \end{array}

Then TNN has following error estimates:

dimension	$e_{L^2}$	$e_{H^1}$
5	1.089e-07	1.920e-07
10	1.040e-07	1.502e-07
20	8.646e-08	1.203e-07

$(\lambda,u)\in \mathbb R\times H_0^1(\Omega)$ such that

\begin{array}{r} {\begin{aligned} - Δ u & = λ u, & x \in & (0, 1)^{d}, \\ u & = 0, & x \in & \partial [0, 1]^{d} . \end{aligned} \end{array}

Then TNN has following error estimats:

dimension	$e_\lambda$	$e_{L^2}$	$e_{H^1}$
5	1.339e-14	2.980e-08	1.215e-07
10	1.656e-14	9.541e-	1.588e-07
20	3.744e-14	1.626e-07	2.509e-07

$(\lambda, u)$ such that

\begin{array}{r} - Δ u + \sum_{i = 1}^{d} x_{i}^{2} = λ u, x \in R^{d} . \end{array}

Then TNN has following error estimates:

dimension	$e_\lambda$	$e_{L^2}$	$e_{H^1}$
5	5.370e-13	4.131e-07	8.664e-07
10	1.245e-13	3.213e-07	4.733e-07
20	3.523e-13	7.768e-07	9.746e-07

Papers:

Y. Wang, P. Jin and H. Xie, Tensor neural network and its numerical integration. arXiv preprint arXiv:2207.02754, 2022.
Y. Wang, Y. Liao and H. Xie, Solving Schrödinger equation using tensor neural network. arXiv:2209.12572, 2022.
Y. Wang and H. Xie, Computing multi-eigenpairs of high-dimensional eigenvalue problems using tensor neural networks, Journal of Computational Physics，Volume 506, 1 June 2024, 112928 (arXiv:2305.12656, 2023).
Y. Wang and H. Xie, Solving high dimensional partial differential equations using tensor type discretization and optimization process, arXiv:2211.16548, 2022.
Y. Wang, Z. Lin, Y. Liao, H. Liu and H. Xie, Solving high dimensional partial differential equations using tensor neural network and a posteriori error estimators, arXiv:2311.02732 , 2023.

Finite element method and its applications

We prove the lower bound results for the error estimates of the general piecewise polynomial approximations in the general norm sense and on the general meshes. Based on the lower bound results, we derive the necessity of the higher order polynomial interpolation in the superconvergence and extrapolation methods.
The lower bound results also provide a mathematical tool to prove the asymptotic lower bound results of the eigenvalues by some nonconforming finite element methods.

Papers:

Qun Lin, Hehu Xie and Jinchao Xu, Lower Bounds of the Discretization for Piecewise Polynomials, Math. Comp., 83 (2014), 1-13.
Shanghui Jia, Fusheng Luo and Hehu Xie, A Posterior Error Analysis for the Nonconforming Discretization of Stokes Eigenvalue Problem, Acta Mathematica Sinica, English Series, 30(6) (2014), 949–967.
Qun Lin, Fusheng Luo and Hehu Xie, A posteriori error estimator and lower bound of a nonconforming finite element method, Journal of Computational and Applied Mathematics, 256(1), pages 243-254, 2014.
Qun Lin and Hehu Xie, Recent results on Lower bounds of eigenvalue problems by nonconforming finite element methods, Inverse Problems and Imaging, Volume 7, No. 3, 2013, 795-811.
Qin Li, Qun Lin and Hehu Xie,Nonconforming finite element approximations of the Steklov eigenvalue problem and its lower bound approximations, Applications of Mathematics, Volume 58, Issue 2, 2013, pp 129-151.
F.Luo, Qun Lin and Hehu Xie (谢和虎), Computing the lower and upper bounds of Laplace eigenvalue problem: by combining conforming and nonconforming finite element methods, Science China Mathematics, Volume 55, Issue 5, pp 1069-1082, 2012.
Q. Lin and H. Xie, The asymptotic lower bounds of eigenvalue problems by nonconforming finite element methods, Mathematics in Practice and Theory, 42 (11) (2012), 219–226.(In Chinese with English title and abstract)
Q. Lin, H. Xie, F. Luo, Y. Li and Y. Yang, Stokes eigenvalue approximations from below with nonconforming mixed finite element methods, Mathematics in Practice and Theory, 40(19)(2010), 157-168. (In Chinese, English title and abstract)

Numerical computing and its software developing

FEM_MATLAB: a Matlab software that implements the multilevel correction method;

GCGE: a software for solving large scale eigenvalue problems;

OpenPFEM: a parallel finite element analysis software(1D,2D,3D).

PASE: a parallel augmented subspace eigensolver.

特征值问题数值算法讲义: 课程特征值问题数值算法的讲义, 相应的视频如下: 特征值问题数值算法视频1 (Bilibili网站), 特征值问题数值算法视频2 (Bilibili网站);

All distributions

Numerical Method for Differential-Integral Equations and Ordinary Differential Equations

Functional equation and delay differential equation: We study the collocation method for a class of functional equations with vanish delays and the corresponding Volterra functional integral equations, the discontinuous Galerkin method for the delay differential equations of pantograph type and the corresponding interesting superconvergence, the hp discontinuous Galerkin (hp-DG) method for delay differential equations with nonlinear delay.

Papers:

Ran Zhang, Benxi Zhu and Hehu Xie, Spectral methods for weakly singular Volterra integral equations with pantograph delays，Frontiers of Mathematics in China, Vol. 8, Issue 2, 2013, pp 281-299
$hp$ Discontinuous Galerkin Method for Delay Differential Equations with Nonlinear Vanishing Delay, SIAM J. Sci. Comput., 35(3), 2013, A1604–A1620.
H. Xie, R. Zhang and H. Brunner, Collocation Methods for General Volterra Functional Integral Equations with Vanishing Delays, SIAM Journal on Scientific Computing, 33(6) (2011), 3303-3332.
Q. Huang, H. Xie and H. Brunner, Superconvergence of a discontinuous Galerkin solutions for delay differential equations of pantograph type, SIAM Journal on Scientific Computing， 33(5) (2011), 2664–2684.
H. Brunner, Hehu Xie and R. Zhang, Analysis of collocation solutions for a class of functional equations with vanishing delays, IMA Journal of Numerical Analysis, 31(2011), 698-718.
H. Brunner, Q. Huang and H. Xie, Discontinuous Galerkin methods for delay differential equations of pantograph type, SIAM J. NUMER. ANAL., Vol. 48, No. 5, pp. 1944–1967, 2010.
Q. Huang and Hehu Xie, Superconvergence of Galerkin solutions for Hammerstein equations, International Journal of Numerical Analysis & Modeling, 2009， Volume 6, Number 4, Pages: 696-710.

Finite Element Methods: Accuracy and Improvement

We give asymptotic eigenvalue error expansions and extrapolation schemes for the Laplace eigenvalue problem on the classical four types of uniform triangular meshes.
We analyze the asymptotic error expansions and extrapolation for the second order elliptic eigenvalue problem and Stokes eigenvalue problem by the mixed finite element method.
We analyze the superconvergence and extrapolation on the general triangular meshes.
We analyze the superconvergence of the Stokes problem by local projection stabilization methods.

Papers:

Shanghui Jia， Hongtao Chen and Hehu Xie, A posteriori error estimator for eigenvalue problems by mixed finite element method, Science China Mathematics,Volume 56, Issue 5, 2013, pp 887-900
Qun Lin and Hehu Xie, Extrapolation of the finite element method on general meshes, International Journal of Numerical Analysis and Modeling Computing and Information, Vol. 10, Number 1, 2013, pp. 139-153.
Qun Lin and Hehu Xie (谢和虎), A Superconvergence result for mixed finite element approximations of the eigenvalue problem, ESAIM: Mathematical Modelling and Numerical Analysis, Volume 46/Issue 04, pp 797-812, 2012.
Qun Lin and Hehu Xie, A type of finite element gradient recovery method based on vertex-edge-face interpolation: The recovery rechnique and superconvergence property, East Asian Journal on Applied Mathematics, 1(3) (2011), 248-263.
S. Jia, H. Xie and X. Yin, A type of finite element gradient recovery method based on vertex-edge interpolation, Mathematics in Practice and Theory, 41(6) (2011), 239-243. (In Chinese, English title and abstract)
Qun Lin and Hehu Xie, Superconvergence measurement for General meshes by linear finite element method, Mathematics in Practice and Theory, 41(1)(2011), 138-152. (In Chinese, English title and abstract)
H. Eichel, L. Tobiska and H. Xie, Supercloseness and superconvergence of stabilized low order finite element discretizations of the Stokes problem, Mathematics of Computation, 80(274)(2011), 697–722.
$-\Delta u = \lambda\rho u$ by linear finite element on different triangular meshes, International Journal of Information and Systems Sciences, 6(1)(2010), 10-34
Qun Lin and Hehu Xie, Asymptotic error expansion and Richardson extrapolation of eigenvalue approximations for second order elliptic problems by the mixed finite element method, Applied Numerical Mathematics, 59(8)(2009), 1884-1893.
S. Jia, Hehu Xie, X. Yin and S. Gao, Approximation and eigenvalue extrapolation of Stokes eigenvalue problem by nonconforming finite element methods, Applications of Mathematics, 54(1)(2009), 1-15.
Hehu Xie and S. Jia, Extrapolation for the second order elliptic problems by mixed finite element methods in three dimensions, International Journal of Numerical Analysis and Modeling, 5(1)(2008), 112-131.
S. Jia, Hehu Xie, X. Yin and S. Gao, Approximation and eigenvalue extrapolation of biharmonic eigenvalue problem by nonconforming finite element methods, Numerical Methods for Partial Differential Equations, 24(2) ,435-448,2008.
X. Yin, Hehu Xie, S. Jia and S. Gao, Asymptotic expansions and extrapolations of eigenvalues for the stokes problem by mixed finite element methods, Journal of Computational and Applied Mathematics, 215(1)(2008), 127-141
Hehu Xie, Extrapolation of the Nédélec element for the Maxwell equations by the mixed finite element method, Advances in Computational Mathematics, 29(2) (2008), 135-145.
Hehu Xie and S. Gao, Superconvergence of the least-squares mixed finite element approximations for the second order elliptic problems, International Journal of Information and Systems Sceiences, Vol.3 (2) (2007), 277-282.
V. Shaidurov and Hehu Xie, Richardson extrapolation for eigenvalue of discrete spectral problem on general mesh, Computational Technologies, Vol. 12 No. 3(2007), 24-37.