-
Download: GCGE-main.tar.gz
-
Documentation
Parallel Solution of Large-scale Sparse Linear Eigenvalue Problems
Ax=λx Ax=λBxGCG Algorithm
The generalized conjugate gradient algorithm is a type of subspace projection method, which uses the block damping inverse power idea to generate triple blocks [X,P,W], where X saves the current eigenvector approximation, P saves the information from previous iteration step, and W saves vectors from X by the inverse power iteration with some CG steps. We name this method as generalized conjugate gradient algorithm since the structure of triple blocks [X,P,W] is similar to that of conjugate gradient method.
Optimal techniques
GCGE is a currently active project, we are striving to bring new improvements and new algorithms on a regular basis. Here we list the main improvements we have made.
The converged eigenpairs do not participate the subsequent iteration;
The sizes of P and W are set to be blockSize, which is equal to numEigen/5 as default;
The shift is selected dynamically when solving W;
The large scale orthogonalization to V is transformed into the small scale orthogonalization to P and a large scale orthogonalization to W;
A moving mechnism is used when computing large scale eigenvalue problem.
FAQ
Please contribute to our FAQ if you feel some questions are missing by emailing the Xie-group.
Related papers
Last updated 2022-12-06 23:10:10 PST
|
Overview
The package GCGE (Generalized Conjugate Gradient Eigensolver) is a software for solving large scale eigenvalue problems. GCGE is written by C language and constructed with the way of matrix-free and vector-free. So far, the eigensolvers for the matrices which are stored in dense format, compressed row/column sparse format or are supported in MATLAB, Hypre, PETSc and PHG. It is noted that there is no need to copy the built-in matrices and the vectors from these softwares/libraries to the GCGE package.
Software
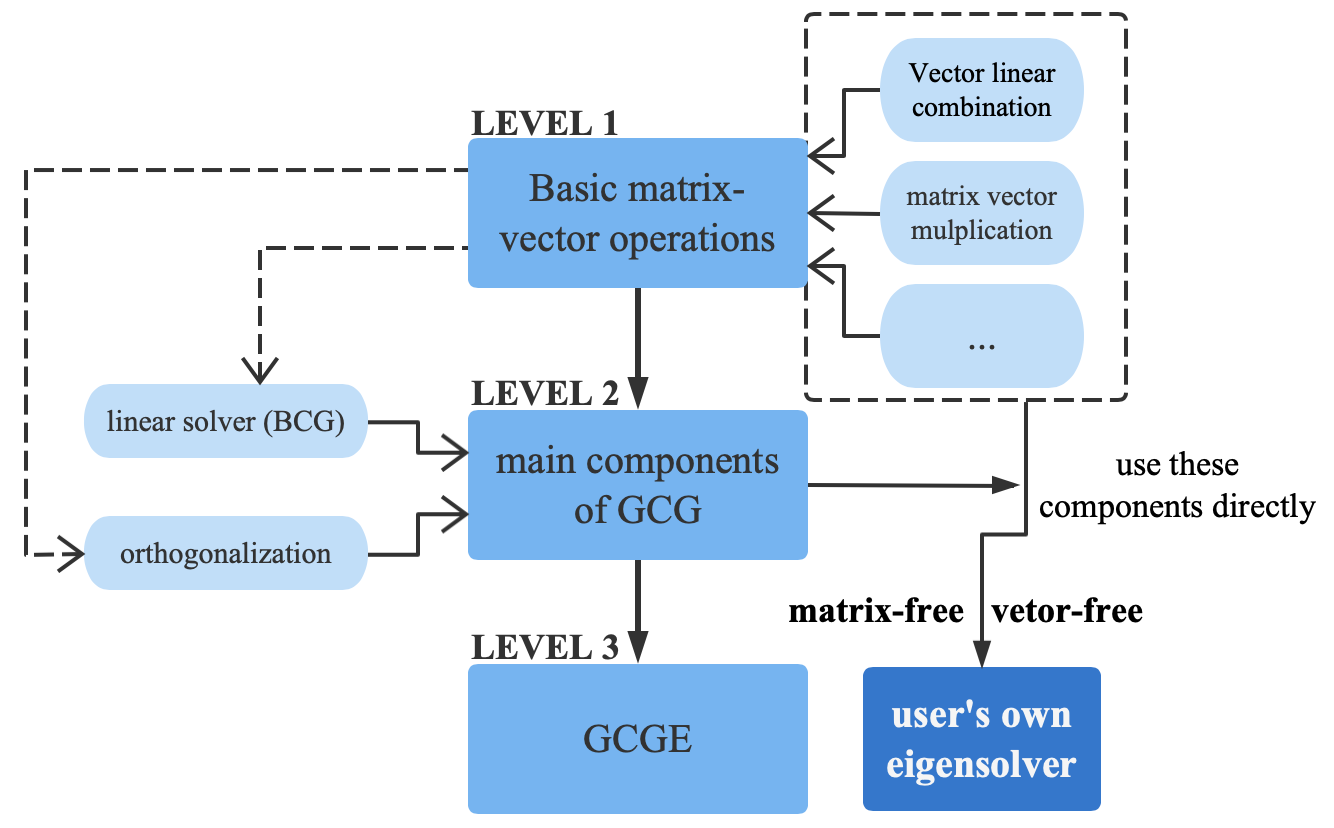
We can divide GCGE into three levels:
-
LEVEL1--Basic matrix-vector operations: vector linear combination(y = ax + by), matrix vector multiplication(y = Ax),...
-
LEVEL2--main algorithms: linear solver(block conjugate gradient method), orthogonalization(block modified Gram-Schmidt method)
-
LEVEL3--GCG algorithm
-
If you modify the source for these routines we ask that you change the name of the routine and comment the changes made to the original.
-
We will gladly answer any questions regarding the software. If a modification is done, however, it is the responsibility of the person who modified the routine to provide support.
download & install
GCGE is a freely-available software package. It is available at https://github.com/Materials-Of-Numerical-Algebra/GCGE .
The license used for the software is the modified MIT license, see:
Like all software, it is copyrighted. It is not trademarked, but we do ask the following:
Configure and install: install_GCGE