|
“油藏模拟与波动问题及其反问题计算”
基础研究
应隆安 孙家昶 黄云清 白中治 羊丹平
 应隆安的工作 应隆安的工作
非结构网格上多维双曲型守恒律方程的有限元方法研究,与许进超等合作,设计了一种非线性守恒型有限元格式(一阶、二阶),证明了在一般网格下收敛于初值问题的熵解,对于均匀网格与光滑解,近似解在空间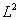 和 和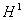 中有二阶收敛性,这是迄今为止同时证明了具有这两种收敛性的唯一计算格式。Chorin-Marsden公式的收敛性为一公开问题,应隆安得到了在一般二维区域上的收敛性结果,阶为1/4,与半平面上的结果吻合。与杨彤,朱长江,张心婷等合作,对于Majda模型,证明了强爆轰波的渐近稳定性,研究了投影—有限差分方法,证明了在粗网格上的收敛性与解的定性性质,特别是对于点火温度的依赖性。 中有二阶收敛性,这是迄今为止同时证明了具有这两种收敛性的唯一计算格式。Chorin-Marsden公式的收敛性为一公开问题,应隆安得到了在一般二维区域上的收敛性结果,阶为1/4,与半平面上的结果吻合。与杨彤,朱长江,张心婷等合作,对于Majda模型,证明了强爆轰波的渐近稳定性,研究了投影—有限差分方法,证明了在粗网格上的收敛性与解的定性性质,特别是对于点火温度的依赖性。
在2003年第五届国际工业应用数学大会上应邀做45分钟的报告“Interface
Problems and their Applications”。 查看... [返回]
 孙家昶的工作 孙家昶的工作
在网格与广义Fourier变换研究方面,孙家昶提出了“非传统结构化网格”的概念;对于二维的三向网格(平行六边形网格)及三维的四向网格(平行十二面体网格),建立了相应的广义Fourier变换,Fourier
级数等较系统的理论,在数学上已推广到任意高维的情况,实现了相应非张量积区域上的快速算法(即广义FFT),并推出了相应的公开并行软件包FFTH。[返回]
 黄云清的工作 黄云清的工作
黄云清等利用单位分解来“粘结”不同的子空间,成功的解决了非匹配网格上的有限元问题;将多层线性化与Cascade迭代有机结合,设计的“多层逐次迭代法”使得求解非线性问题可以在几乎最优的工作量下完成;对于p-Laplacian
问题,通过在新的空间意义下求出的最速下降方向(相当于对经典意义下的最速下降法进行某种预处理),得到了一种与网格规模无关的迭代算法,极大的改善了此类问题的求解效率。
《混合有限元高效算法及其在油藏数值模拟中的应用》获2004年湖南省科技进步二等奖,黄云清是第二完成人。
[返回]
 白中治的工作 白中治的工作
针对油藏模拟中产生的具有特殊结构的代数方程组,提出并深入研究了有效的迭代算法与理论。这项工作的主要创新点是基于系数矩阵的对称与反对称分裂设计了一类实用有效的迭代算法(HSS),并建立了相应的收敛理论。将HSS算法与预处理技术有机地结合,得到了一类能够有效求解鞍点(或KKT)线性方程组的预处理HSS算法。将HSS算法发展到了非对称矩阵的正规与反对称分裂以及正定与反对称分裂上,得到了关于非对称线性代数方程组的NSS算法和PSS算法,证明了这类算法的收敛性。这类算法在具体计算中取得了很好的效果。[返回]
 羊丹平的工作 羊丹平的工作
Euler和Navier-Stokes方程组的多尺度解的数学模型和数值方法的研究,是多尺度分析中最具挑战性的问题和困扰流体科学界多年的最困难问题之一。羊丹平与侯一钊教授合作研究,基本学术思想是发展多尺度展开和均匀化理论,系统地刻画雷诺张量中大尺度和小尺度互动结构,在理论上搞清楚大尺度和小尺度互动的机理,基于这个结构建立工程上适用的大尺度模拟模型和数值方法。最近他们已发现了一些大尺度和小尺度互动的关系,
在理论上已经取得了系统的分析结果。[返回]
|