|
|
|
|
- "Node patch" boundary element method (NBEM):
The boundary element patches constructed around nodes and supposed
to be constant, we call this a constant "node patch" BEM.
This BEM considerably improves the speed performance
compared with the constant element and linear element methods.
A simple way to construct these new patches is illustrated in right figure
 in which an example ``node patch" at the i-th node
that has five neighboring elements is constructed.
All the centroids {O_l, l=1,...5} of the five adjacent triangles and
the midpoints {C_l, l=1,...5}
of the attached five edges are listed, and then the area formed
by {O_1,C_1,O_2,C_2,... O_5,C_5,O_1} is the new patch that we want.
Therefore, there is one third of the area of each neighboring
triangle occupied by the ``node patch" $\Delta S_i$.
The other patches are similarly constructed. All the node patches
connect and cover the whole surface.
Now, the far-field integrals on the new patch
in which an example ``node patch" at the i-th node
that has five neighboring elements is constructed.
All the centroids {O_l, l=1,...5} of the five adjacent triangles and
the midpoints {C_l, l=1,...5}
of the attached five edges are listed, and then the area formed
by {O_1,C_1,O_2,C_2,... O_5,C_5,O_1} is the new patch that we want.
Therefore, there is one third of the area of each neighboring
triangle occupied by the ``node patch" $\Delta S_i$.
The other patches are similarly constructed. All the node patches
connect and cover the whole surface.
Now, the far-field integrals on the new patch
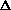 Si
become Si
become
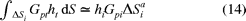
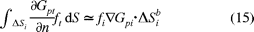
where, supposing all neighboring elements of ith node form
a set {L},
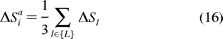
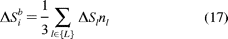
where nl is the unit normal vector
of the lth neighboring
element,  Sl is the area of
the lth adjacent triangular element,
and &Delta Sib here should also be considered as a vector. As in the constant element treatment, for near-patch integration, a
normal quadrature method is used. Similar treatments apply
to the integrations for the kernel u and its derivative, as well
as for the other second-derivative terms if the dBIEs are used. Sl is the area of
the lth adjacent triangular element,
and &Delta Sib here should also be considered as a vector. As in the constant element treatment, for near-patch integration, a
normal quadrature method is used. Similar treatments apply
to the integrations for the kernel u and its derivative, as well
as for the other second-derivative terms if the dBIEs are used.
There are three main advantages of this ``node patch"
treatment in the BEM. First, as aforementioned, the unknowns are
reduced by almost half relative to the constant element
method. Second, straightforward storage of matrix coefficients, because
it is easy to locate the ``near points" (local list) of any
node for integration. This, though not explicit, but
maybe the main advantage of NBEM. Third, convenient to
use interpolation method as a postprocess to compute the potential
and its gradient (not only the normal derivative)
at any position near or on the molecular surface, e.g., for
stress and force calculation (see the reference).
Reference:
Lu, B. Z. and McCammon, J. A. Improved boundary element methods for Poisson-Boltzmann electrostatic potential and force calculations. J. Chem. Theory. Comput. 3(3):1134–1142, 2007. link .
|
|
 in which an example ``node patch" at the i-th node
that has five neighboring elements is constructed.
All the centroids {O_l, l=1,...5} of the five adjacent triangles and
the midpoints {C_l, l=1,...5}
of the attached five edges are listed, and then the area formed
by {O_1,C_1,O_2,C_2,... O_5,C_5,O_1} is the new patch that we want.
Therefore, there is one third of the area of each neighboring
triangle occupied by the ``node patch" $\Delta S_i$.
The other patches are similarly constructed. All the node patches
connect and cover the whole surface.
Now, the far-field integrals on the new patch
in which an example ``node patch" at the i-th node
that has five neighboring elements is constructed.
All the centroids {O_l, l=1,...5} of the five adjacent triangles and
the midpoints {C_l, l=1,...5}
of the attached five edges are listed, and then the area formed
by {O_1,C_1,O_2,C_2,... O_5,C_5,O_1} is the new patch that we want.
Therefore, there is one third of the area of each neighboring
triangle occupied by the ``node patch" $\Delta S_i$.
The other patches are similarly constructed. All the node patches
connect and cover the whole surface.
Now, the far-field integrals on the new patch
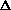 Si
become
Si
become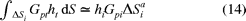
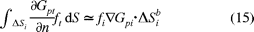
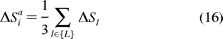
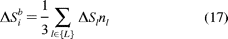
 Sl is the area of
the lth adjacent triangular element,
and &Delta Sib here should also be considered as a vector. As in the constant element treatment, for near-patch integration, a
normal quadrature method is used. Similar treatments apply
to the integrations for the kernel u and its derivative, as well
as for the other second-derivative terms if the dBIEs are used.
Sl is the area of
the lth adjacent triangular element,
and &Delta Sib here should also be considered as a vector. As in the constant element treatment, for near-patch integration, a
normal quadrature method is used. Similar treatments apply
to the integrations for the kernel u and its derivative, as well
as for the other second-derivative terms if the dBIEs are used.