研究介绍

本人目前的研究兴趣主要在于偏微分方程数值算法、特征值问题的数值算法、神经网络机器学习、有限元方法、积微分方程的数值算法以及他们在实际问题中的应用，喜欢数值算法的构造及其算法的理论分析。

特征值问题的数值算法

众所周知，在科学研究与工程实际中存在着大量的非线性问题，比如特征值问题、带不等式约束的最优控制问题、相场模型等。尤其特征值问题是个基本而又有特色的问题，大量出现于量子力学、复杂结构共振模态分析、材料科学中。相对于边值问题的求解，特征值问题和非线性方程的求解更加复杂和困难，内存开销往往也更大，研究特征值问题和非线性方程的高效算法及其理论具有重要的理论和实际意义。

基于对有限元中Aubin-Nitsche技巧的新认识，我们首次设计了求解特征值问题和非线性方程的扩展子空间算法和多水平校正算法，并且给出了相应的理论分析，显著提高了求解非线性方程和特征值问题的效率。利用低维有限元空间，我们通过构造一个低维的子空间把定义在细网格上高维的特征值问题或非线性方程的求解转换成细网格上线性边值问题的求解和低维子空间上特征值问题或非线性方程的求解。由于避免了在细网格上直接求解高维的特征值问题或非线性方程，扩展子空间算法和多水平校正算法显著地提高了它们的求解效率。特别地，结合我们提出的张量组装技术，当求解多项式形式的非线性方程(包括特征值问题)时，所设计的扩展子空间算法和多水平校正算法的渐近计算量可以达到最优且与非线性迭代次数无关，这是求解非线性问题所能达到的最优程度。这种方式改变了自Brandt(1983)和Hackbusch(1979)等提出的求解非线性方程的多重网格算法计算量不能达到与非线性迭代次数无关的缺点。
该方法提供了一种求解特征值问题和非线性方程新的迭代方法和新的并行方法，使得求解特征值问题的计算量可以达到线性依赖特征值个数的程度，为设计出求解实际科学研究中特征值问题的线性标度算法提供了算法和理论的基础。甚至在充分并行计算的环境下，设计的算法可以同时求解不同的特征对而使得计算时间与所求解的特征对个数无关。
目前为止，已使用扩展子空间算法和多水平校正算法设计了求解线性特征值问题、带不等式约束的最优控制问题、Bose-Einstein凝聚的基态问题、电子结构中的Kohn-Sham方程、反散射特征值问题、多尺度特征值问题和半线性椭圆方程等的多水平或多重网格算法。根据扩展子空间算法,构造了求解大规模特征值问题的并行扩展子空间算法软件包PASE (Parallel Augmented Subspace Eigensolver),见: https://github.com/pase2017/pase.

软件下载:

FEM_MATLAB (一个可以进行多重校正算法的Matlab软件包)。
PASE (一个可以进行扩展子空间并行求解特征值问题的C软件包)。
介绍材料
课程《特征值问题数值算法》的讲义: 特征值问题数值算法讲义;
相应的视频如下: 特征值问题数值算法视频1 (Bilibili网站), 特征值问题数值算法视频2 (Bilibili网站);
相关论文:
Xiaole Han, Hehu Xie and Fei Xu, A cascadic multigrid method for eigenvalue problem, Journal of Computational Mathematics, 35(1) (2017), 7-90.
Shanghui Jia, Hehu Xie, Manting Xie and Fei Xu, A full multigrid method for nonlinear eigenvalue problems, Sci China Math, 59 (2016), 2037–2048.
Hehu Xie and Manting Xie, A multigrid method for ground state solution of Bose-Einetein condensates, Commun. Comput. Phys., 19(3) (2016), 648-662.
Hongtao Chen, Hehu Xie and Fei Xu, A full multigrid method for eigenvalue problems, Journal of Computational Physics,322 (2016),747-759.
Xiaole Han, Yu Li, Hehu Xie and Chunguang You, Local and parallel finite element algorithm based on multilevel discretization for eigenvalue problems, International Journal of Numerical Analysis & Modeling, 13(1) (2016),73-89.
Hehu Xie and Tao Zhou, A multilevel finite element method for Fredholm integral eigenvalue problems,Journal of Computational Physics,303 (2015),173-184.
Hongtao Chen, Yunhui He, Yu Li and Hehu Xie, A multigrid method for eigenvalue problems based on shifted-inverse power technique, European Journal of Mathematics, 1(1) (2015), 207-228.
Xiaole Han, Yu Li and Hehu Xie, A multilevel correction method for Steklov eigenvalue problem by nonconforming finite element methods, Numerical Mathematics: Theory, Methods and Applications, 8(03) (2015), 383-405.
谢和虎, 非线性特征值问题的多重网格算法, 中国科学:数学, 45(8) (2015), 1193-1204.
Qun Lin, Hehu Xie and Fei Xu, Multilevel correction adaptive finite element method for semilinear elliptic equation, Application of Mathematics, 60(5) (2015), 527-550.
Wei Gong, Hehu Xie and Ningning Yan, A multilevel correction method for optimal controls of elliptic equation, SIAM J. Sci. Comput., 37(5) (2015), A2198-A2221.
Qun Lin, Fusheng Luo and Hehu Xie, A multilevel correction method for Stokes eigenvalue problems and its application, Mathematical Methods in the Applied Sciences, 38(18) (2015), 4540-4552.
Qun Lin and Hehu Xie, A multi-level correction scheme for eigenvalue problems, Mathematics of Computation, 84(291) (2015), 71-88.
Hehu Xie, A type of multilevel method for the Steklov eigenvalue problem, IMA J. Numer. Anal., 34(2) (2014), 592-608.
Hehu Xie, A multigrid method for eigenvalue problem, Journal of Computational Physics, 274(1), 2014, pages 550-561.
Xia Ji, Jiguang Sun and Hehu Xie, A multigrid method for Helmholtz transmission eigenvalue problems, Journal of Scientific Computing, 60(2), pages: 276-294, 2014.
Qun Lin and Hehu Xie (谢和虎), A multilevel correction type of adaptive finite element method for Steklov eigenvalue problems, Proceedings of the International Conference Applications of Mathematics 2012, pp. 134-143.
Qun Lin and Hehu Xie, An observation on Aubin-Nitsche Lemma and its applications, Mathematics in Practice and Theory, 41(17) (2011), 247-258.(In Chinese, English title and abstract)

代数特征值问题求解算法

随着现代国防研究的需要，材料科学和工程科技向高精尖方向发展，需要求解的特征值问题的规模越来越大。我们根据阻尼块反幂法的思想设计了求解代数特征值问题的广义共轭梯度算法GCGE(General Conjugate Gradient Eigensolver)，同时也实现了相应的并行软件包。一方面目前存在的代数特征值解法器基本上都是针对串行计算机建立的，并不能很好地适应当前的大规模并行计算的要求。另一方面，工程研究中的实际问题往往需要代数解法器具有非常好的稳定性和效率，目前通用的解法器都不满足此要求。基于这两方面的考虑，我们在并行计算的框架下，基于阻尼块反幂法的思想设计了求解代数特征值问题的新型代数解法器GCGE。进一步设计了稳定、高效、高可扩展性的并行向量正交化算法、Rayleigh-Ritz求解算法和移动技术来减少GCGE求解特征值问题的计算时间和内存消耗。在天河二号升级系统(国产飞腾处理器)上进行过测试。通过对实际问题和国际通用测试集的验证，我们设计的特征值解法器比国际上通用的解法器具有更好的稳定性、更高的计算效率和可扩展效，更低的内存消耗，更适合在高性能并行计算机上求解大规模特征值问题的大量特征对，同时更好的数值稳定性使得GCGE更适合求解性质复杂的病态特征值问题。软件包是以matrix-free和vector-free的方式建立的，相应的软件包可见:https://github.com/pase2017/GCGE-1.0

GCGE Matlab接口

GCGE的基本操作是针对CSC格式的矩阵实现的，依赖的标准库是Matlab的BLAS和LAPACK。解法器源码用C实现，采用混合编程的形式在Matlab里对GCGE进行调用，编译选项如下


mex -v  -R2018a -I../src -I../app ../app/app_matlab.c ...
    ../src/ops.c ../src/ops_multi_vec.c ../src/ops_orth.c ../src/ops_multi_grid.c ...
    ../src/ops_lin_sol.c ../src/ops_eig_sol_gcg.c ../src/ops_eig_sol_pas.c ...
    ../app/app_lapack.c ../app/app_ccs.c ../app/app_pas.c -lmwlapack -lmwblas

数值测试

$10^{-8}$ , Matlab的eigs和lobpcg调用方式如下


xxxxxxxxxx
%%
%eigs
tic;meval=eigs(A,nev,'smallestabs','Tolerance',1e-8);toc
%%
%lobpcg
X0=randn(size(A,1),nev);
maxiter=500; tol=1e-8;
tic;[blockVectorX,leval,failureFlag] = lobpcg(X0,A,tol,maxiter);

具体的测试结果如下：

矩阵	矩阵维数	目标特征对个数	GCGE 计算时间	LOBPCG 计算时间	eigs 计算时间
Si5H12	19,896	10	2.69	3.12	52.72
Ga3As3H12	61,349	10	26.45	40.53	684.05
Andrews	60,000	10	6.01	11.48	63.49
Si34H36	97,569	10	25.18	46.90	-
Ga10As10H30	113,081	10	32.57	81.05	-
Ga41As41H72	268,096	10	181.51	216.76	-
Ga19As19H42	133,123	10	61.49	97.33	-

矩阵	矩阵维数	目标特征对个数	GCGE 计算时间	LOBPCG 计算时间	eigs 计算时间
Si5H12	19,896	100	37.58	56.14	99.27
Ga3As3H12	61,349	100	272.94	981.20	361.12
Andrews	60,000	100	58.31	125.26	141.26
Si34H36	97,569	100	200.81	273.40	-
Ga10As10H30	113,081	100	247.05	819.63	-
Ga41As41H72	268,096	100	357.66	1007.53	-
Ga19As19H42	133,123	100	1038.19	5497.40	-

表格说明

以上稀疏矩阵均来自于稀疏矩阵库
"-"表示matlab在计算过程中闪退或者超过8h运行无结果
Matlab版本为R2018a，测试环境为: macOS Sonoma 14.0，处理器为2.6GHz六核Intel Core i7
LOBPCG为BLOPEX中实现的版，源码见https://github.com/lobpcg/blopex/
表格中的计算时间均不含稀疏矩阵格式转换的时间

相关论文：

Y. Li， Hehu Xie， R. Xu， C. You and N. Zhang， A parallel generalized conjugate gradient method for large scale eigenvalue problems，CCF Transactions on High Performance Computing， 2 (2020)，111–122.
张宁、李瑜、谢和虎、徐然、游春光，一种求解特征值问题的广义共轭梯度算法，中国科学:数学，51(8) (2021), 1297-1320.
Y. Li， Z. Wang and Hehu Xie， GCGE: a package for solving large scale eigenvalue problems by parallel block damping inverse power method ， CCF Transactions on High Performance Computing， https://doi. org/10. 1007/s42514-023-00135-1，2023.

神经网络机器学习

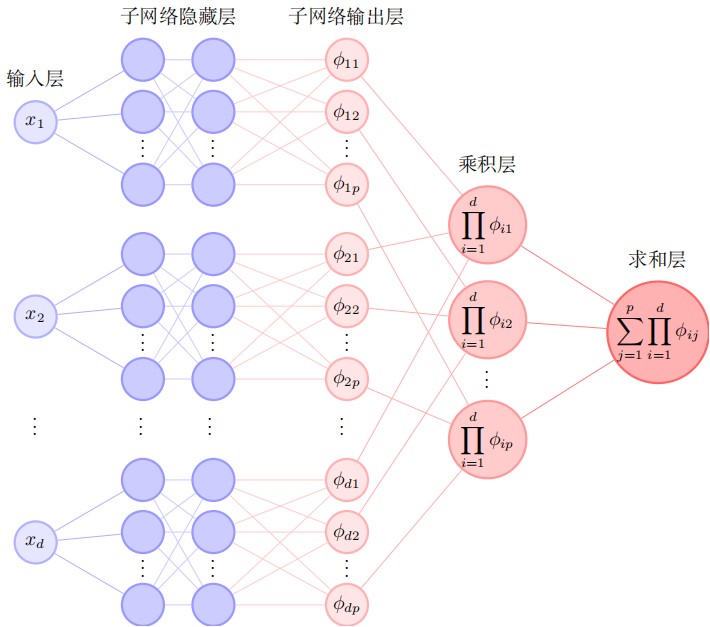
目前主要关注设计张量型神经网络来求解高维问题，设计了求解高维问题的张量神经网络(TNN). 张量神经网络函数是利用张量的思想作用到相互关联的神经网络函数而构造出来的一类函数。张量神经网络设计的目的是为了摆脱计算损失函数对Monte-Carlo采样的依赖，将其中的高维积分转化成简单的一维积分，从而可使用经典的数值积分格式得到高精度的高维积分，进而使得相应的机器学习方法的精度远超其它类型的机器学习方法。高维张量神经网络函数积分的计算量可以达到多项式量级，在求解高维微分方程的时候摆脱维数灾难。另外，高维积分的高精度可以导致损失函数计算的高精度，从而可以提升机器学习求解高维偏微分方程的稳定性和效率。

The number of layers and neurons in each layer, the selections of activation functions and other hyperparameters can be different in different subnetworks. TNN is defined as follows:

\begin{array}{r} (1) & Ψ (x; Θ) = \sum_{j = 1}^{p} c_{j} {\hat{ϕ}}_{1, j} (x_{1}; θ_{1}) {\hat{ϕ}}_{2, j} (x_{2}; θ_{2}) \dots {\hat{ϕ}}_{d, j} (x_{d}; θ_{d}) = \sum_{j = 1}^{p} c_{j} \prod_{i = 1}^{d} {\hat{ϕ}}_{i, j} (x_{i}; θ_{i}), \end{array}

$c=\{c_j\}_{j=1}^{p}$ $\Theta=\{c,\theta_1,\cdots,\theta_d\}$ $i=1,\cdots,d,j=1,\cdots,p$ $\widehat\phi_{i,j}(x_i,\theta_i)$ is a normalized functions as follows:

\begin{array}{r} (2) & {\hat{ϕ}}_{i, j} (x_{i}, θ_{i}) = \frac{ϕ_{i, j} (x_{i}, θ_{i})}{∥ ϕ_{i, j} (x_{i}, θ_{i}) ∥_{L^{2} (Ω_{i})}} . \end{array}

由于张量神经网络函数可以进行高精度的高维积分，这使得我们可以充分结合传统数值算法中的方法来设计求解高维问题的机器学习算法，比如我们可以根据有限元方法中的后验误差估计和自适应的思想来设计求解高维问题基于后验误差估计子的机器学习算法，使得精度可以达到跟经典算法求解低维问题的精度一样。

除了我们自己对TNN的应用之外，也被如下的文章用来求解 20,000维含有耦合谐振子势能的Schr"{o}dinger方程的求解，

Z. Hu, K. Shukla, G. E. Karniadakis and K. Kawaguchi, Tackling the curse of dimensionality 768 with physics-informed neural networks, arXiv:2307.12306v5, 2024.

也被下面的文章用来求解高维的Fokker-Planck方程：

T. Wang, Z. Hu, K. Kawaguchi, Z. Zhang and G. E. Karniadakis, Tensor neural networks for high-dimensional Fokker-Planck equations, arXiv:2404.05615v1, 2024.

被下面的文章用来构造求解高维含时方程的高精度机器学习方法：

T. Kao, J. Zhao and L. Zhang, pETNNs: partial evolutionary tensor neural networks for solving time-dependent partial differential equations, arXiv:2403.06084v1, 2024.

$u$ 满足如下的边值问题

\begin{array}{r} {\begin{aligned} - Δ u & = (d + 3) π^{2} \sum_{k = 1}^{d} \sin (2 π x_{k}) \cdot \prod_{i \neq k}^{d} \sin (π x_{i}), & x \in & (- 1, 1)^{d}, \\ u & = 0, & x \in & \partial [- 1, 1]^{d} . \end{aligned} \end{array}

TNN方法可以得到如下的误差结果:

dimension	$e_{L^2}$	$e_{H^1}$
5	1.089e-07	1.920e-07
10	1.040e-07	1.502e-07
20	8.646e-08	1.203e-07

$(\lambda,u)\in \mathbb R\times H_0^1(\Omega)$ such that

\begin{array}{r} {\begin{aligned} - Δ u & = λ u, & x \in & (0, 1)^{d}, \\ u & = 0, & x \in & \partial [0, 1]^{d} . \end{aligned} \end{array}

TNN方法可以得到如下的误差结果:

dimension	$e_\lambda$	$e_{L^2}$	$e_{H^1}$
5	1.339e-14	2.980e-08	1.215e-07
10	1.656e-14	9.541e-	1.588e-07
20	3.744e-14	1.626e-07	2.509e-07

$(\lambda, u)$ such that

\begin{array}{r} - Δ u + \sum_{i = 1}^{d} x_{i}^{2} = λ u, x \in R^{d} . \end{array}

TNN方法可以得到如下的误差结果:

dimension	$e_\lambda$	$e_{L^2}$	$e_{H^1}$
5	5.370e-13	4.131e-07	8.664e-07
10	1.245e-13	3.213e-07	4.733e-07
20	3.523e-13	7.768e-07	9.746e-07

相关论文:

Y. Wang, P. Jin and H. Xie, Tensor neural network and its numerical integration. arXiv preprint arXiv:2207.02754, 2022.
Y. Wang, Y. Liao and H. Xie, Solving Schrödinger equation using tensor neural network. arXiv:2209.12572, 2022.
Y. Wang and H. Xie, Computing multi-eigenpairs of high-dimensional eigenvalue problems using tensor neural networks, Journal of Computational Physics，Volume 506, 1 June 2024, 112928 (arXiv:2305.12656, 2023).
Y. Wang and H. Xie, Solving high dimensional partial differential equations using tensor type discretization and optimization process, arXiv:2211.16548, 2022.
Y. Wang, Z. Lin, Y. Liao, H. Liu and H. Xie, Solving high dimensional partial differential equations using tensor neural network and a posteriori error estimators, arXiv:2311.02732 , 2023.

偏微分方程的数值算法

We prove the lower bound results for the error estimates of the general piecewise polynomial approximations in the general norm sense and on the general meshes. Based on the lower bound results, we derive the necessity of the higher order polynomial interpolation in the superconvergence and extrapolation methods.
The lower bound results also provide a mathematical tool to prove the asymptotic lower bound results of the eigenvalues by some nonconforming finite element methods.

相关论文:

Qun Lin, Hehu Xie and Jinchao Xu, Lower Bounds of the Discretization for Piecewise Polynomials, Math. Comp., 83 (2014), 1-13.
Shanghui Jia, Fusheng Luo and Hehu Xie, A Posterior Error Analysis for the Nonconforming Discretization of Stokes Eigenvalue Problem, Acta Mathematica Sinica, English Series, 30(6) (2014), 949–967.
Qun Lin, Fusheng Luo and Hehu Xie, A posteriori error estimator and lower bound of a nonconforming finite element method, Journal of Computational and Applied Mathematics, 256(1), pages 243-254, 2014.
Qun Lin and Hehu Xie, Recent results on Lower bounds of eigenvalue problems by nonconforming finite element methods, Inverse Problems and Imaging, Volume 7, No. 3, 2013, 795-811.
Qin Li, Qun Lin and Hehu Xie,Nonconforming finite element approximations of the Steklov eigenvalue problem and its lower bound approximations, Applications of Mathematics, Volume 58,Issue 2, 2013, pp 129-151.
F.Luo, Qun Lin and Hehu Xie (谢和虎), Computing the lower and upper bounds of Laplace eigenvalue problem: by combining conforming and nonconforming finite element methods, Science China Mathematics, Volume 55, Issue 5, pp 1069-1082, 2012.
Q. Lin and H. Xie, The asymptotic lower bounds of eigenvalue problems by nonconforming finite element methods, Mathematics in Practice and Theory, 42 (11) (2012), 219–226.(In Chinese with English title and abstract)
Q. Lin, H. Xie, F. Luo, Y. Li and Y. Yang, Stokes eigenvalue approximations from below with nonconforming mixed finite element methods, Mathematics in Practice and Theory, 40(19)(2010), 157-168. (In Chinese, English title and abstract)

相场模型和对流扩散问题的数值算法

Convergence theory for spectral deferred correction method: We give the convergence analysis for the SDC method.
Numerical method for phase field methods (time adaptivity, mixed finite element method).
Numerical method for convection-diffusion-reaction equations.
Method to define the metric tensor.

相关论文:

Yu Li, Qun Lin and Hehu Xie, A parallel method for population balance equations based on the method of characteristics, Proceedings of the International Conference Applications of Mathematics, 2013, pp. 140-149.
Tao Tang, Hehu Xie and Xiaobo Yin, High-Order Convergence of Spectral Deferred Correction Methods on General Quadrature Nodes, Journal of Scientific Computing Volume 56, Issue 1, 2013, pp 1-13
Xiaobo Yin and Hehu Xie, $L^p$ norm, Journal of Computational Physics, 256(1), Pages: 543-562, 2014.
Zhonghua Qiao, Tao Tang and Hehu Xie, Error analysis of a mixed finite element method for molecular beam epitaxy model, SIAM J. Numer. Anal., 53(1) (2015), 184-205.
Fusheng Luo, Tao Tang and Hehu Xie, Parametert-free time adaptivity based on energy evolution for Cahn-Hilliard equation, Commun. Comput. Phys., 19(05) (2016), 1542-1563.
N. Ahmed, G. Matthies, L. Tobiska and H. Xie, Discontinuous Galerkin time stepping with local projection stabilization for transient convection-diffusion-reaction problems，Comput. Methods Appl. Mech. Engrg., 200 (2011), 1747-1756.

积微分方程和常微分方程数值算法

Functional equation and delay differential equation: We study the collocation method for a class of functional equations with vanish delays and the corresponding Volterra functional integral equations, the discontinuous Galerkin method for the delay differential equations of pantograph type and the corresponding interesting superconvergence, the hp discontinuous Galerkin (hp-DG) method for delay differential equations with nonlinear delay.

Papers:

Ran Zhang, Benxi Zhu and Hehu Xie, Spectral methods for weakly singular Volterra integral equations with pantograph delays，Frontiers of Mathematics in China, Vol. 8, Issue 2, 2013, pp 281-299.
$hp$ Discontinuous Galerkin Method for Delay Differential Equations with Nonlinear Vanishing Delay, SIAM J. Sci. Comput., 35(3), 2013, A1604–A1620.
H. Xie, R. Zhang and H. Brunner, Collocation Methods for General Volterra Functional Integral Equations with Vanishing Delays, SIAM Journal on Scientific Computing, 33(6) (2011), 3303-3332.
Q. Huang, H. Xie and H. Brunner, Superconvergence of a discontinuous Galerkin solutions for delay differential equations of pantograph type, SIAM Journal on Scientific Computing， 33(5) (2011), 2664–2684.
H. Brunner, Hehu Xie and R. Zhang, Analysis of collocation solutions for a class of functional equations with vanishing delays, IMA Journal of Numerical Analysis, 31(2011), 698-718.
H. Brunner, Q. Huang and H. Xie, Discontinuous Galerkin methods for delay differential equations of pantograph type, SIAM J. NUMER. ANAL., Vol. 48, No. 5, pp. 1944–1967, 2010.
Q. Huang and Hehu Xie, Superconvergence of Galerkin solutions for Hammerstein equations, International Journal of Numerical Analysis & Modeling, 2009， Volume 6, Number 4, Pages: 696-710.

高效有限元方法

We give asymptotic eigenvalue error expansions and extrapolation schemes for the Laplace eigenvalue problem on the classical four types of uniform triangular meshes.
We analyze the asymptotic error expansions and extrapolation for the second order elliptic eigenvalue problem and Stokes eigenvalue problem by the mixed finite element method.
We analyze the superconvergence and extrapolation on the general triangular meshes.
We analyze the superconvergence of the Stokes problem by local projection stabilization methods.

相关论文:

Shanghui Jia， Hongtao Chen and Hehu Xie, A posteriori error estimator for eigenvalue problems by mixed finite element method, Science China Mathematics,Volume 56, Issue 5, 2013, pp 887-900.
Qun Lin and Hehu Xie, Extrapolation of the finite element method on general meshes, International Journal of Numerical Analysis and Modeling Computing and Information, Vol. 10, Number 1, 2013, pp. 139-153.
Qun Lin and Hehu Xie (谢和虎), A Superconvergence result for mixed finite element approximations of the eigenvalue problem, ESAIM: Mathematical Modelling and Numerical Analysis, Volume 46/Issue 04, pp 797-812, 2012.
Qun Lin and Hehu Xie, A type of finite element gradient recovery method based on vertex-edge-face interpolation: The recovery rechnique and superconvergence property, East Asian Journal on Applied Mathematics, 1(3) (2011), 248-263.
S. Jia, H. Xie and X. Yin, A type of finite element gradient recovery method based on vertex-edge interpolation, Mathematics in Practice and Theory, 41(6) (2011), 239-243. (In Chinese, English title and abstract)
Qun Lin and Hehu Xie, Superconvergence measurement for General meshes by linear finite element method, Mathematics in Practice and Theory, 41(1)(2011), 138-152. (In Chinese, English title and abstract)
H. Eichel, L. Tobiska and H. Xie, Supercloseness and superconvergence of stabilized low order finite element discretizations of the Stokes problem, Mathematics of Computation, 80(274)(2011), 697–722.
$-\Delta u = \lambda\rho u$ by linear finite element on different triangular meshes, International Journal of Information and Systems Sciences, 6(1)(2010), 10-34
Qun Lin and Hehu Xie, Asymptotic error expansion and Richardson extrapolation of eigenvalue approximations for second order elliptic problems by the mixed finite element method, Applied Numerical Mathematics, 59(8)(2009, 1884-1893.
S. Jia, Hehu Xie, X. Yin and S. Gao, Approximation and eigenvalue extrapolation of Stokes eigenvalue problem by nonconforming finite element methods, Applications of Mathematics, 54(1)(2009), 1-15.
Hehu Xie and S. Jia, Extrapolation for the second order elliptic problems by mixed finite element methods in three dimensions, International Journal of Numerical Analysis and Modeling, 5(1)(2008), 112-131.
S. Jia, Hehu Xie, X. Yin and S. Gao, Approximation and eigenvalue extrapolation of biharmonic eigenvalue problem by nonconforming finite element methods, Numerical Methods for Partial Differential Equations, 24(2) ,435-448,2008.
X. Yin, Hehu Xie, S. Jia and S. Gao, Asymptotic expansions and extrapolations of eigenvalues for the stokes problem by mixed finite element methods, Journal of Computational and Applied Mathematics, 215(1)(2008), 127-141
Hehu Xie, Extrapolation of the Nédélec element for the Maxwell equations by the mixed finite element method, Advances in Computational Mathematics, 29(2) (2008), 135-145.
Hehu Xie and S. Gao, Superconvergence of the least-squares mixed finite element approximations for the second order elliptic problems, International Journal of Information and Systems Sceiences, Vol.3 (2) (2007), 277-282.
V. Shaidurov and Hehu Xie, Richardson extrapolation for eigenvalue of discrete spectral problem on general mesh, Computational Technologies, Vol. 12 No. 3(2007), 24-37.

研 究 介 绍

特征值问题的数值算法

代数特征值问题求解算法

神经网络机器学习

偏微分方程的数值算法

相场模型和对流扩散问题的数值算法

积微分方程和常微分方程数值算法

高效有限元方法

研究介绍