波动方程真振幅叠前深度偏移

70年代John Clacrbout提出的单程波方程偏移，以及其后发展的一系列单程波方程偏移方法，以地下构造成像为目标，其所依据的单程波方程只保证了波传播的运动学特征，并不保证其动力学特征，因此不能保证其真振幅。张关泉（1993）应用波场分裂的思想，将波动算子因子分解，导出了更为确切的拟微分算子（平方根算子）表达的单程波方程及其微分—积分方程组的表达形式。这个新形式的单程波方程与原先导出的单程波方程不同之处在于：（1）它在±90^o倾角范围内都是精确的；（2）在它的表达式中出现了一项新的振幅控制项，保证了波传播的动力学特征，即保证了其真振幅。本世纪初，在此基础上，发展了波动方程真振幅偏移（Yu Zhang，Guanquan Zhang ，Norman Bleistein，True amplitude wave equation migration arizing from true amplitude one-waymwave equations，Inverse Problems 19（2003）1113-1138）

波动方程真振幅偏移分二个步骤，即波场延拓和成像。

下行波延拓

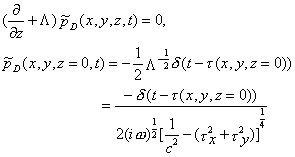上行波延拓

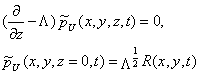其中

为记录数据。

定义

反射系数成像公式

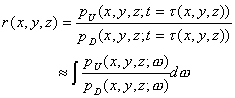其中和分别为象征

的拟微分算子，为介质中声波传播速度，为地面记录。上述波场延拓方程可以写成微分积分方程组形式，以便于实现数值计算。

真振幅波动方程偏移与常规的波动方程偏移不同之处在于：

（1）下行波地面定解条件与常规情况不同，由于出现^-1，它不仅改变了振幅，而且还出现45^o相位差；

（2）成像条件必须是反卷积形式p_U / p_D ，其中p_U，p_D是由上、下行波方程的解转换而来。

（3）在同相轴上偏移结果的振幅恰好为此处的反射系数（依赖于入射角），因此可用于AVA，AVO分析。

　　数值实验：

　　在V=2000+0.3Z的介质中,分别于1000m ,2000m ,3000m 和4000m深处设置了四个反射层，假设反射系数均为1，产生了合成记录，利用此合成记录作真振幅偏移，其成像结果见下图。
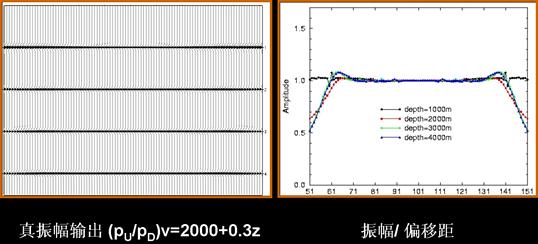