Research on nolocal minimal graphs
Nolocal minimal graphs. Joint work with R. H. Nochetto (UMD, USA) and J. P. Borthagaray (UdelaR, Uruguay).
Links to our papers:
Finite element discretizations of nonlocal minimal graphs: convergence,
Finite element algorithms for nonlocal minimal graphs.
The study of this nonlocal nonlinear problem, which can be regarded as a nonlocal version of the classical Plateau problem, began with the seminal papers by (C. Imbert 2009 Interfaces Free Bound.) and by (L. A. Caffarelli, J.-M. Roquejoffre, O. Savin 2010 Comm. Pure Appl. Math.)
In the context that the nonlocal minimum set is the subgraph below a function $u$, finding an $s$-minimal set for $s \in (0, 1/2)$ is equivalent to finding the minimizer of the following strictly convex energy
\[\small I_s[v] := \iint_{Q_{\Omega}} F_s \left( \frac{v(x)-v(y)}{|x-y|}\right) \frac{dxdy}{|x-y|^{d+2s-1}} , \text{ where } Q_{\Omega} = \left( \mathbb{R}^d \right)^2 \setminus \left( {\Omega}^c \right)^2,\, F_s(\rho) := \int_0^{\rho} \frac{\rho - r}{(1+r^2)^{(d+1+2s)/2}} dr,\]supplemented with the Dirichlet boundary condition $u = g$ in $\Omega^c$. Taking the first variation of the energy functional, we get the weak formulation that $u$ satisfies
\begin{equation} \small a(u,v) := \iint_{Q_{\Omega}} G_s\left(\frac{u(x)-u(y)}{|x-y|}\right) \frac{(u(x)-u(y))(v(x)-v(y))}{|x-y|^{d+1+2s}}dxdy = 0, \text{ where } G_s(\rho) := F_s’(\rho)/\rho, \label{E:WeakForm-NMS-Graph} \end{equation}
for any $v$ s.t. $v = 0$ in $\Omega^c$. This equation can be interpreted as a degenerate fractional diffusion problem of order $s+1/2$ with weights depending on $u$. We also consider the prescribed nonlocal mean curvature problem where the right-hand side in $\eqref{E:WeakForm-NMS-Graph}$ is replaced by an $L^2$ inner product between the test function $v$ and the prescribed curvature.
We study this problem from a numerical point of view in Finite element discretizations of nonlocal minimal graphs: convergence and Finite element algorithms for nonlocal minimal graphs. we propose and analyze the discretization of problem $\eqref{E:WeakForm-NMS-Graph}$ using continuous, piecewise linear, Lagrangian finite elements on shape-regular meshes over bounded domains. We prove that our discrete solution converges in $W^{2r}_1(\Omega)$ for all $r < s$, where $W^{2s}_1(\Omega)$ is the natural energy space. In addition, we introduce a geometric notion of error that recovers a weighted $L^2$-discrepancy between the normal vectors to the graphs in the limit $s \to 1/2$. Under realistic regularity assumptions, we derive error bounds for this novel geometric quantity as well.
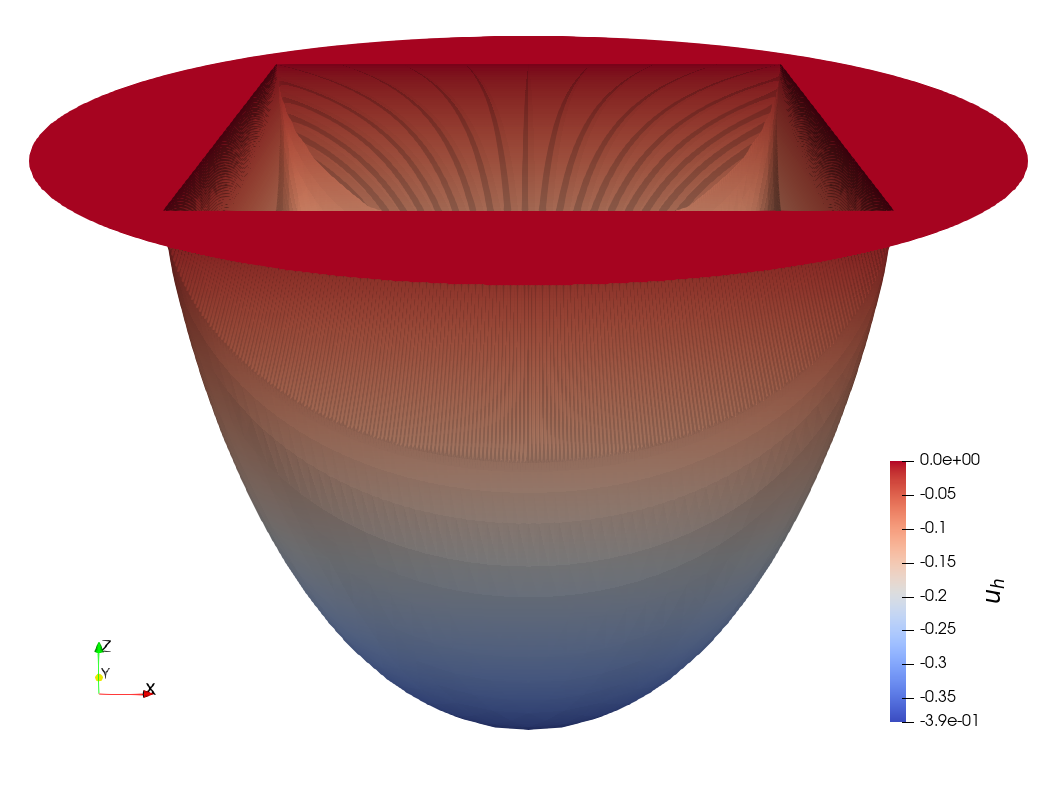
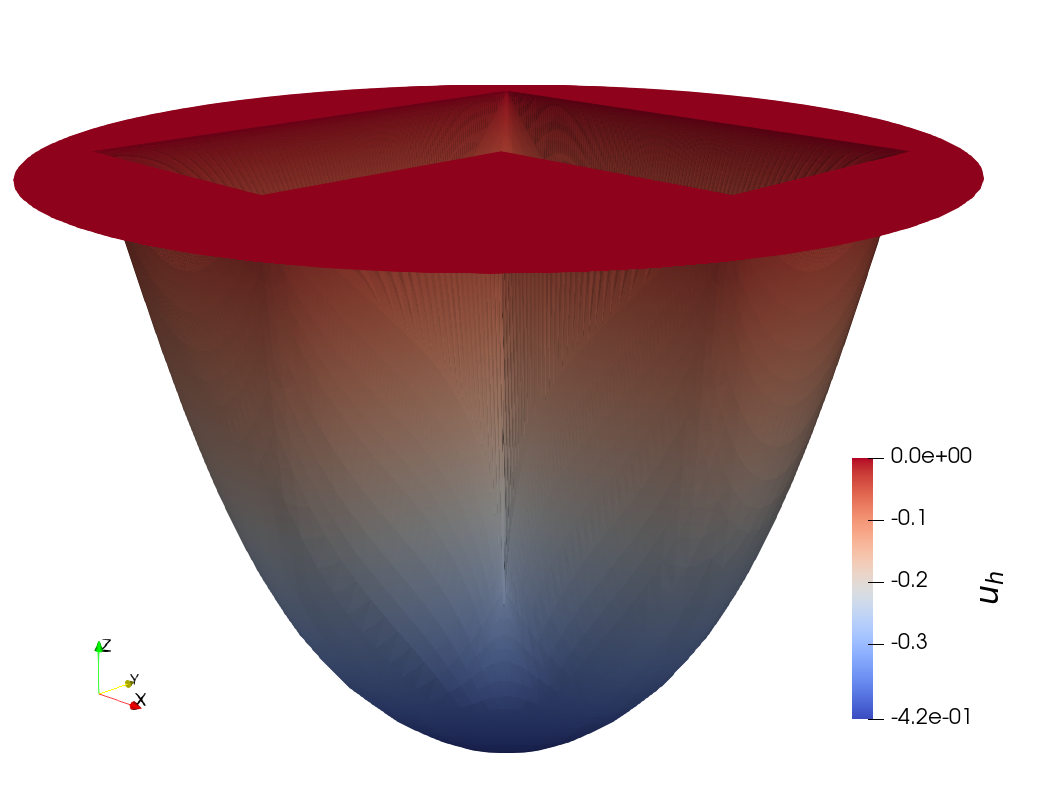
It is worth pointing out that nonlocal minimal graphs, in general, admit the stickiness phenomenon, that is, the solutions $u$ are discontinuous across the boundary. See below for some interesting numerical experiments of stickiness.